表磁如何计算?
磁感应强度,通常称为表磁,是衡量磁钢性能的关键指标,它指的是磁钢表面的磁场强度。在许多需要利用空间磁场的技术领域,表磁或特定点的磁感应强度常常被视为一项关键的技术规范。需要注意的是,表磁是具有方向性的,通常所指的数值是垂直于磁极面的表磁值。
那么,表磁是否能够被计算出来呢?如果可以,我们应该怎么做?
这是许多人都感兴趣的问题。在网络上,我们可以找到一些计算公式,同时许多磁性材料制造商的官方网站也提供了计算工具,以方便用户进行计算。然而,使用过这些工具的人可能会发现,这些公式或工具通常只能计算圆柱形和长方体形状磁铁的表磁,且计算的是中心位置的表磁。
对于其他形状的磁铁,计算是否变得复杂?最高表磁的计算是否也变得困难?确实,准确计算表磁是一项极具挑战性且复杂的任务。对于圆柱形和长方体磁体,我们通常假设磁场分布是理想的且对称的,中心位置的表磁被认为是理想状态下垂直于磁极面的。在气隙中的磁导率和磁铁的磁导率都被假定为相等,且值为1.0。在这些假设的基础上,我们才能得到相对简单的计算方法。可以参考TDK提供的计算公式来进行计算。
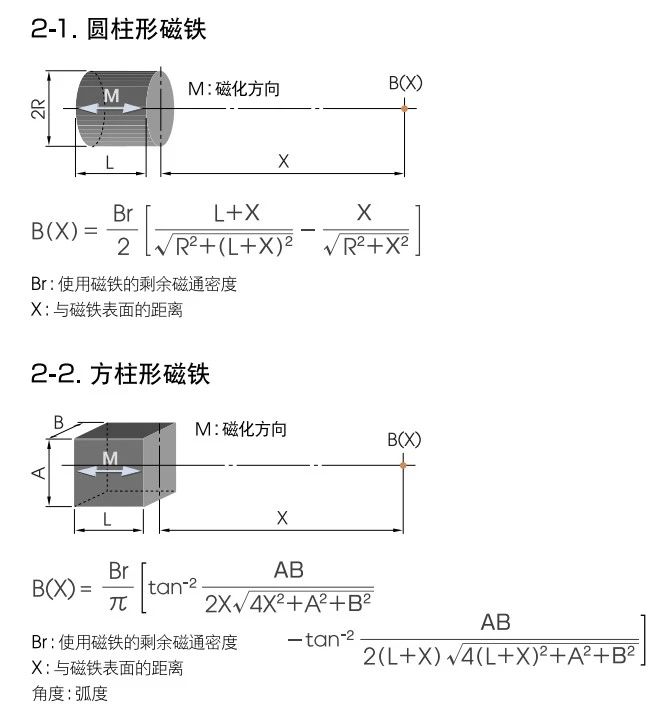
表磁作为衡量磁钢性能的关键指标,其测量和计算的准确性对于应用领域至关重要。尽管基于理论公式制作的Excel计算器为计算提供了便利,但在实际应用中,人们常发现计算值与实测值之间存在较大差异。以N50 D10*10mm的磁体为例,即使在理想条件下使用高斯计测量,实测值也很难达到理论计算值。这种情况引发了对计算公式准确性的疑问。
要深入理解这一问题,我们需要回顾公式的适用条件和假设。首先,公式中的X值代表计算点到磁铁表面的距离。尽管在实际操作中,我们尽可能让测量探头紧贴磁铁表面,但探头的保护壳会引入一定的误差。例如,常用的日本KANETEC高斯计探头的霍尔芯片就覆盖有约0.2mm厚的透明保护壳。此外,成品磁体表面的镀层也会对磁场产生屏蔽作用,导致测量值降低。例如,镍铜镍镀层的厚度一般为0.02mm,这会对磁场产生影响。因此,在实际测量中,X值需要额外补偿0.4-0.5mm,以更准确地反映实际情况。
然而,影响测量结果的另一个重要因素是磁铁和气隙的磁导率。理论上,公式假设磁铁和气隙的磁导率都等于1.0。虽然空气的磁导率非常接近1.0,但磁铁的磁导率往往更高,尤其是N系列和M系列的钕铁硼磁体,其磁导率常超过1.05,有些甚至达到1.1。磁导率的差异会影响磁场的分布和强度,从而影响测量数据。
要全面理解磁导率对测试数据的影响,我们需要回到退磁曲线的概念:
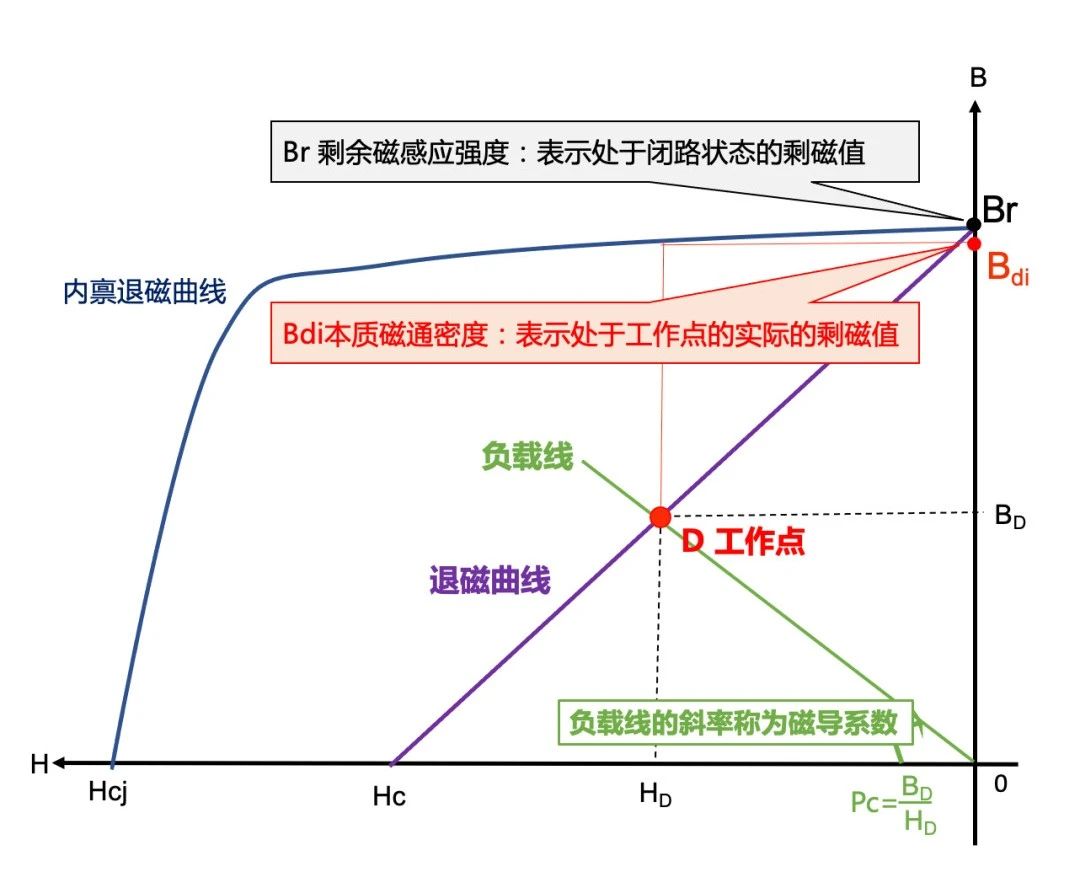
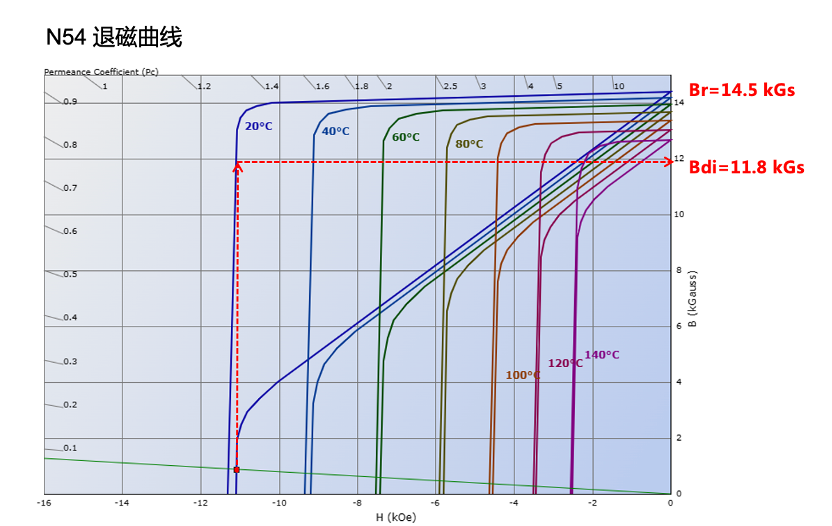
由退磁曲线图可以看出,处于开路状态的磁铁,其实际的剩磁值不是理想的Br值,而是要比Br低,我们称之为本质磁通密度Bdi,其原因就是蓝色的J-H退磁曲线初始状态不是理想的平行于X轴,而是倾斜状态,这样Br数值上一定会大于Hcb,回复磁导率μrec=Br/Hcb就不可能是1.0。还有种情况是B-H线出现拐点,而磁铁的工作点处于拐点以下,这样实际的Bdi就会比Br低很多,这样计算的结果就会偏离实际值较多,如下图,这也解释了为什么N54 20*10*1mm磁体实际的中心表磁不仅远远低于理论计算值,而且还非常不稳定的原因
结合以上,将公式中的Br修正为Bdi,X适当补偿会是比较准确的计算公式,但是实际情况Bdi也是比较难计算的,最佳的方法是根据真实的退磁曲线和Pc值从图上来计算,但是这样也比较繁琐,建议大家按如下思路来计算:
1、首先工作点必须要在B-H退磁曲线拐点以上并保留适当余量,这样特别要注意磁能积45以上的N料,Pc小于0.6的薄片,如果在拐点以下意味着磁性是不稳定的,即使从曲线上推算Bdi来算中心表磁波动也会很大,必须要提高Hcj以维持工作点在拐点以下或者BH线不出现拐点。
2、在第一点能满足的前提下,Bdi=Br∙(Pc+1)/(μrec+Pc) ,μrec根据实际值来定,一般N40以下为1.08-1.1,N40及以上为1.06-1.08,M档为1.05-1.06,H档为1.04,其他为1.03。
最终圆柱形(或趋近圆柱形)和长方形(或趋近长方形)的中心表磁的计算公式分别是:
请注意:所述公式主要针对具有线性退磁特性的永磁材料,例如钕铁硼、钐钴和铁氧体。对于那些具有非线性退磁曲线的永磁材料,比如铝镍钴、铁铬钴以及各类软磁材料,这些公式不适用。此外,对于那些磁化方向不垂直于磁极表面的斜向磁铁,这些计算方法同样不适用。